In this issue, the latest advances in research are shared by the Fundamental & Deep Learning (FDL) team from the Research Center for Applied Mathematics and Machine Intelligence. Currently, the FDL team is devoted to developing fundamental and profound learning methods for complex real physical world problems.

In particular, the team focuses on two fundamental characteristics of the physical world: complexity and dynamics. Complexity demonstrates our limited observations of the world, and there are always a lot of uncertainties beyond our cognition/model; dynamics enables massive data collection after the timeline is extended, but at a particular point in time or in a small time window (corresponding to a specific scenario/problem/task), data we can obtain is extremely scarce and its quality cannot be guaranteed (because of annoying noise, data missing or even malicious tampering). Complexity and dynamics affect our observations of the present world, which in turn affects our decision-making and judgment as well as predictions for the future world.

To this end, the team wants to build agents (that is, our intelligent agents) that can assist with more accurate and robust predictions/decisions. The team explores how agents learn and make decisions based on dynamic open-world scenarios, including exploring basic principles, mechanisms and strategies and designing general-purpose methods and technologies; it not only focuses on deep learning, but also draws on ideas, models and methods in mathematical statistics, such as partial differential equations widely used to describe physical phenomena (e.g. fluid mechanics, electromagnetic fields, and quantum mechanics), and Bayesian approach, a powerful tool for uncertainty analysis and modeling and statistical inference.

Recently, the FDL team has made great progress in interactions between agents and LLMs and solving partial differential equations on unbounded domains, and won the second place of two tracks of CVPR'23 Algorithm Challenge.

The introduction of the research is presented below:

An efficient and cost-effective interaction method between agents and LLMs: When2Ask

Paper Link: https://arxiv.org/abs/2306.03604

Code Link: https://github.com/ZJLAB-AMMI/LLM4RL

Large Language Models (LLMs) encode a vast amount of world knowledge acquired from massive text datasets. Recent studies have demonstrated that LLMs can assist an embodied agent in solving complex sequential decision-making tasks by providing advanced instructions. However, interactions with LLMs may be time-consuming, because LLMs require a significant amount of storage space that most likely will be deployed on the remote cloud servers. In addition, using commercial LLMs can be costly since they are typically charged based on usage frequency.

In this paper, we explore how to enable efficient and cost-effective interactions between an agent and an LLM. We propose When2Ask, a reinforcement learning approach that learns when it is necessary to query LLMs for advanced instructions to accomplish a target task. Experiments on MiniGrid and Habitat embodied environments demonstrate that When2Ask learns to solve target tasks efficiently with only a few necessary interactions with an LLM, and significantly reduces interaction costs in testing environments compared with baseline methods, and the agent's performance becomes more robust in a partially observable environment. See Figure 1 for a general framework of using LLMs for solving complex embodied tasks, and Figure 2 for the specific implementation framework of When2Ask.

This paper was accepted by the Symposium on Large Language Models at the International Joint Conference on Artificial Intelligence (IJCAI) 2023.

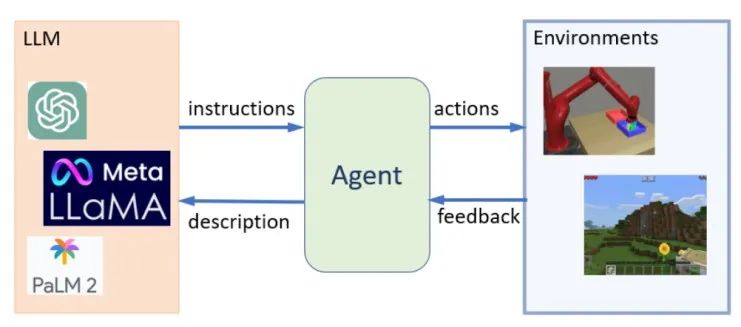
Fig. 1: A general framework of using LLMs for solving complex embodied tasks. The LLMs provide instructions based on state descriptions, and the agent generates actions following these instructions and interacts with the target environment to collect further feedback.

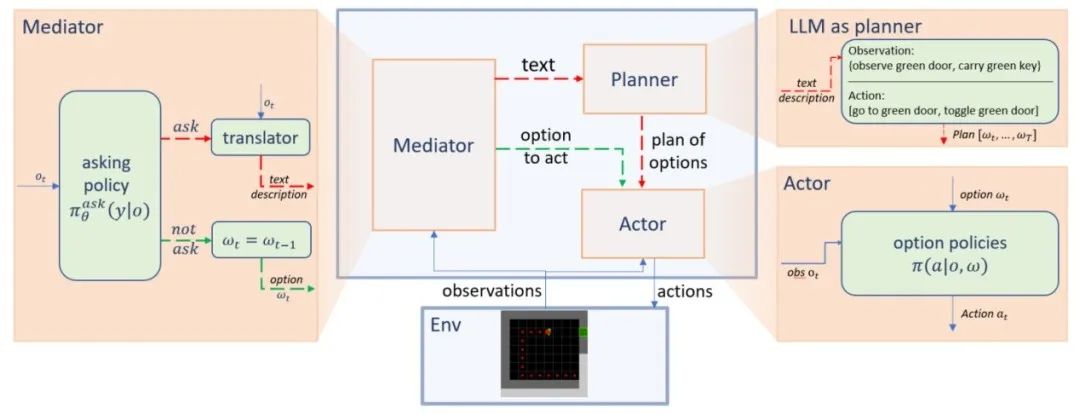
Fig. 2: The adopted Planner-Actor-Mediator framework and an example of the interactions between agent and LLM. LLM acts as a planner. At each time step, the mediator takes the observation result ot as input and decides whether to ask the LLM planner for new instructions or not. When the asking policy decides to ask (as demonstrated with a red dashed line), the translator converts ot into text descriptions, and the planner outputs a new option accordingly for the actor to follow. On the other hand, when the mediator decides to not ask (as demonstrated with a green dashed line), the mediator returns to the actor directly, telling it to continue with the current option.

Using the concept of deep learning to solve partial differential equations on unbounded domains

Paper Link: https://arxiv.org/abs/2309.02446

Many physical phenomena (e.g. wave propagation) can be described as partial differential equations (PDEs) on unbounded domains. The classical scientific computing approach to solving such problems involves truncating them to problems on bounded domains by designing the artificial boundary conditions or perfectly matched layers, which typically requires a large number of manual (numerical computing experts) participation, and the presence of nonlinearity in the equation makes such designs even more challenging. The above classical approach is called a solution based on artificial design.

This paper proposes a novel data generation-based method for solving PDEs on unbounded domains. Specifically, we construct a family of approximate analytical solutions to the target PDE based on its initial conditions and source terms (data generation stage). Then, utilizing these constructed data (including exact solutions, initial conditions and source terms), we train a deep learning model called MIONet (modeling stage), which is capable of handling multiple inputs to learn the mapping from the initial condition and source term to the PDE solution on a bounded domain of interest. Finally, we utilize the generalization ability of this model to predict the solution of the target PDE (utilization model stage). The effectiveness of this method is exemplified by solving the wave equation and the Schrödinger equation defined on unbounded domains. More importantly, the proposed method can deal with nonlinear problems, which has been verified by solving Burger's equation and Korteweg-de Vries (KdV) equation.

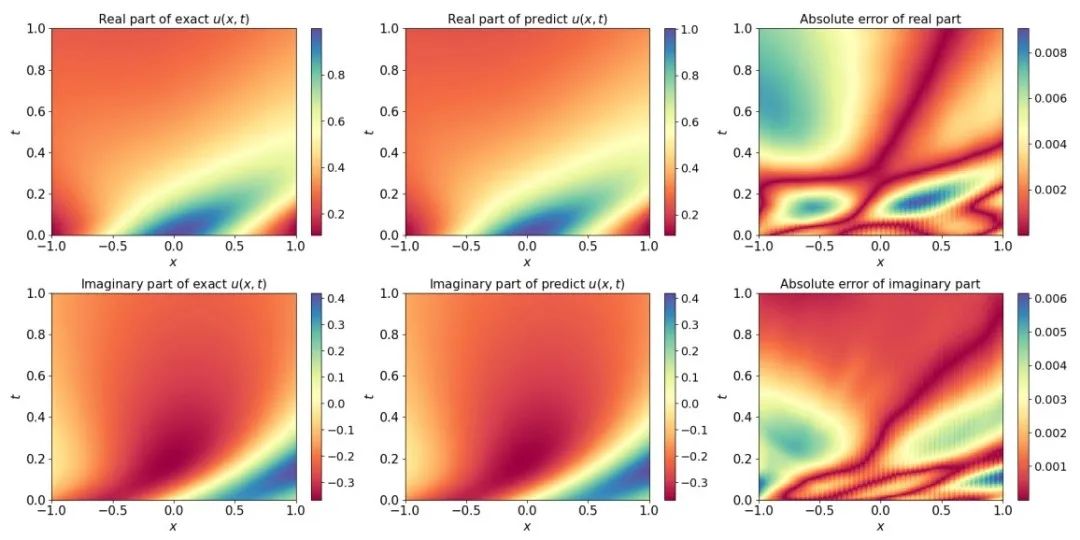
Solving a 1D Schrödinger Equation. Left: exact solution; Middle: predicted solutions generated by this approach; Right: prediction error

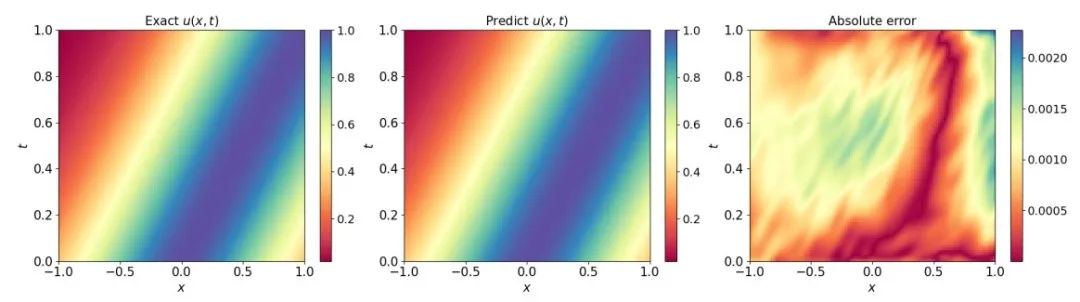
Solving a KdV Equation. Left: exact solution; Middle: predicted solutions generated by this approach; Right: prediction error

The Award-Winning Solution to CVPR'23 SoccerNet Challenge

In the SoccerNet Challenge of the IEEE/CVF Computer Vision and Pattern Recognition Conference 2023 (CVPR'23), WANG Luping, GUO Hao and ZHENG Chaochao won the second place of two tracks, and all the topics/tasks of the competition came from the real physical world, which were characterized by complexity and dynamics. These efforts represent our focus and thinking on complex open-world learning. See the following technical report for details.

Report Link: https://arxiv.org/abs/2306.05772

Code Link: https://github.com/ZJLAB-AMMI/E2E-Spot-MBS

Runner-Up Certificate for Ball Action Spotting Task of CVPR'23 SoccerNet Challenge

Report Link: https://arxiv.org/abs/2305.05454

Code Link: https://github.com/ZJLAB-AMMI/Restormer-Plus

Runner-Up Certificate for CVPR 2023 6^th UG2+ Challenge (Track 3 Single Image Deraining)

The widely adopted Model Ensembling strategy was embedded in our submitted solution. Recently, we proposed Bayesian Dynamic Ensemble of Multiple Models (BDEMM), a model ensembling framework for dynamic open-world scenarios, especially for serialization and online prediction based on time series data, which focuses more on physical-world dynamic time series and uncertainty modeling compared with classical multi-model integration methods. This approach has been used by international and domestic AI research institutions/teams (German Aerospace Center, Karlsruhe Institute of Technology, the State University of New York at Stony Brook, Brain-Computer Interface Research Team from Zhejiang University, etc.) in many different types of practical problems and achieved remarkable results. See the following review paper for details:

Paper Link: https://www.sciencedirect.com/science/article/pii/S0925231223006768

About the FDL Team

The FDL team was established by LIU Bin, a Research Fellow at the Research Center for Applied Mathematics and Machine Intelligence. Their professional background covers deep learning, reinforcement learning, applied mathematics, computational mathematics, computational statistics, Bayesian statistics, computer vision, etc. Oriented toward simplicity, purity, diligence and innovation, the team is committed to exploring profound insights, and developing fundamental algorithms, models and theories, so as to build Zhejiang Lab into a first-class, distinctive fundamental research highland facing the world.